Metallic Ratio Calculator (Golden, Silver, etc.) / Tool

How to use this tool

This is a tool that runs in your browser to calculate precious ratios. It calculates short and long ratios from a single side input. It supports the Golden ratio, Silver ratio, Platinum ratio, Yamato ratio, and Bronze ratio.

• When a numerical value is entered, the “long side with the input value as the short side” and “short side with the input value as the long side” are automatically calculated.
• Calculation results are rounded to the fourth decimal place.

Name	Approximate value of ratio	Summary
Silver ratio	1:1.414	Non-metallic ratio. Used for paper dimensions, etc. It is popular in Japan and is also called Yamato ratio.
Golden ratio	1:1.618	The first metallic ratio.
Platinum ratio	1:1.732	Non-metallic ratio. Equal to the ratio of half the length of the base of an equilateral triangle to the height of the equilateral triangle.
Silver ratio	1:2.414	The second metallic ratio.
Bronze ratio	1:3.303	The third metallic ratio.

What is the metallic ratio?

The metallic ratio is a ratio for which the following equation holds true and is considered to give a sense of stability and beauty.

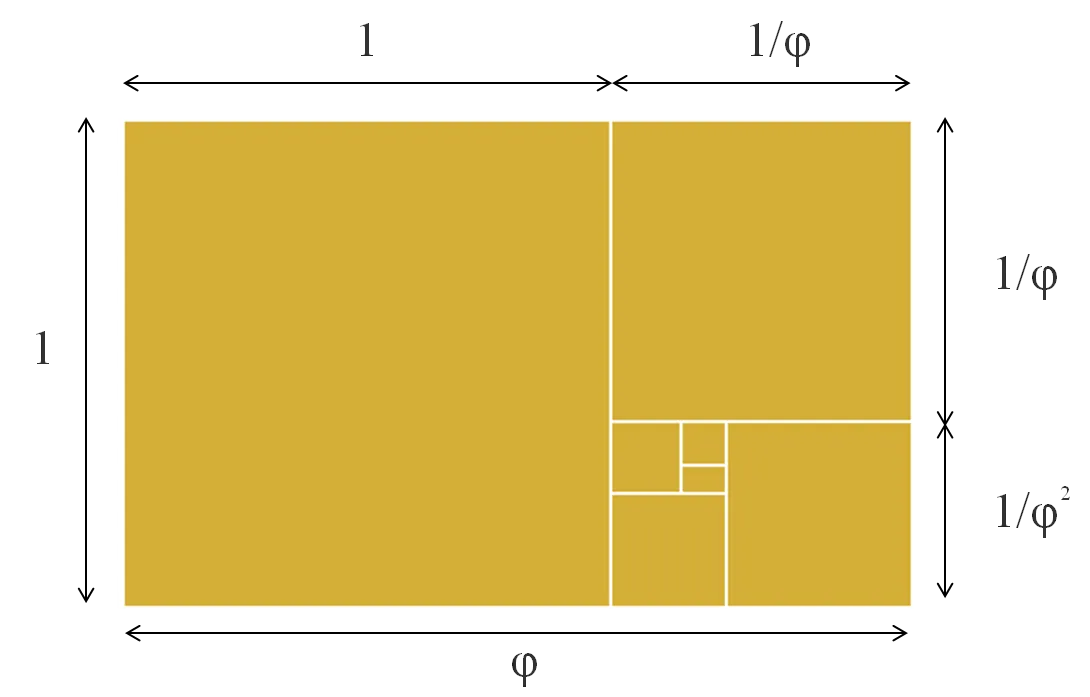
Golden Ratio

The golden ratio is the following ratio.

Approximate value is 1:1.618, approximately 5:8 or 8:13.

${\dfrac {1+{\sqrt {5}}}{2}}$ is called the golden number and is represented by the Greek letter φ (phi).

The golden ratio has long been used in buildings and works of art as a stable and beautiful ratio. Approximations also frequently appear in nature.

• Artifacts: Parthenon, Mona Lisa, Thirty-six Views of Mt. Fuji, Apple’s logo, etc.
• Nature: Nautilus shell spiral, sunflower seed spiral, typhoon and nebula vortex, etc.

Example of Golden Ratio Calculation

e.g. Calculate the short side when the long side is 100

Short side ＝ 100 ÷ ${\dfrac {1+{\sqrt {5}}}{2}}\approx$ 61.803

e.g. Calculate the long side when the short side is 100

Long side ＝ 100 × ${\dfrac {1+{\sqrt {5}}}{2}}\approx$ 161.803

The shape of the tool is a rectangle with the golden ratio of sides (golden rectangle). If the largest square is excluded from this golden rectangle, the remaining rectangle will again be in the ratio of the golden rectangle, thus creating a shape that is forever similar.

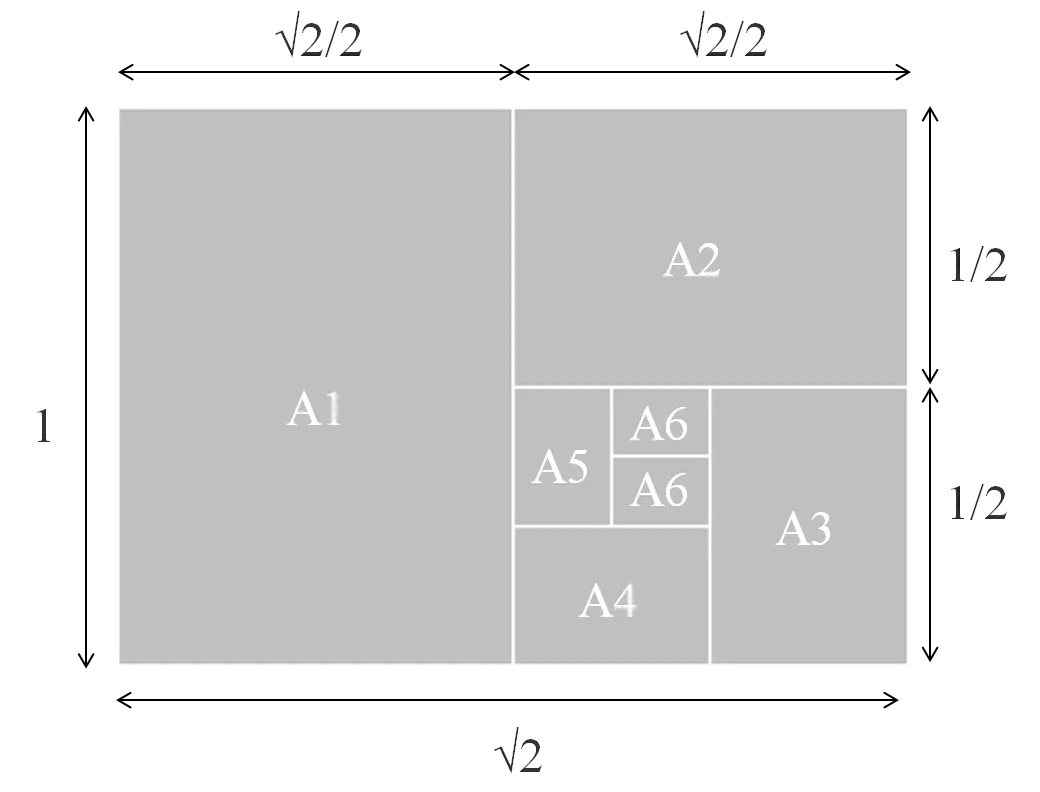
Silver Ratio

There are two types of silver ratios.

1. One of the precious metal ratios

Approximate value is 1:2.414.

2. Yamato ratio

Due to its ${\displaystyle 1:{\sqrt {2}}{}\equiv {}{\sqrt {2}}:2}$ nature, it is used for paper dimensions, etc.

For some reason, Japanese people prefer the silver ratio (Yamato ratio) to the golden ratio, which has been used in buildings for a long time.
e.g. Horyu-ji and Five-storied Pagoda, Choju-Giga, Tokyo Sky Tree, Doraemon, etc.

Example of Silver Ratio Calculation

e.g. Calculate the short side when the long side is 100

Short side ＝ 100 ÷ ${\sqrt {2}}\approx$ 70.711

e.g. Calculate the long side when the short side is 100

Long side ＝ 100 × ${\sqrt {2}}\approx$ 141.421

The shape of this tool is a rectangle whose sides are all bisected by a silver ratio. This is the standard for paper such as A- and B-format.