貴金属比の計算機（黄金比・白銀比など） ／ ツール

ツールの使い方

ブラウザ上で動作する貴金属比の計算するツールで、短辺と長辺を一辺の入力から計算します。黄金比、白銀比、大和比、白金比、青銅比に対応。

• 数値を入力すると、それを「短辺とした場合の長辺」「長辺とした場合の短辺」を自動で計算します。
• 計算結果は小数点第四位で四捨五入します。

名称	比率の近似値	概要
白銀比	1:1.414	非貴金属比。紙の寸法などに用いられる。日本人になじみ深い比率で大和比とも呼ばれる。
黄金比	1:1.618	第1貴金属比。
白金比	1:1.732	非貴金属比。正三角形の底辺の1/2の長さとその正三角形の高さの比に等しい。
白銀比	1:2.414	第2貴金属比。
青銅比	1:3.303	第3貴金属比。

貴金属比とは

貴金属比は以下の数式が成り立つ比率で、安定感や美しさを感じさせるとされています。

黄金比

黄金比（おうごんひ）は以下の比率で、近似値は1:1.618、約5:8または8:13です。

この${\dfrac {1+{\sqrt {5}}}{2}}$を黄金数といい、ギリシア文字のφ （ファイ）で表します。

黄金比は安定した美しい比率として古くから建造物や芸術作品に使われてきました。また、自然界でも近似値がたびたび現れるそうです。

• 人工物：パルテノン神殿、モナリザ、富嶽三十六景、Appleのロゴ、etc
• 自然界：オウムガイの殻の螺旋、ひまわりの種の螺旋、台風や星雲の渦、etc

黄金比の計算例

例）長辺が100の場合の短辺

短辺 ＝ 100 ÷ ${\dfrac {1+{\sqrt {5}}}{2}}$ ≒ 61.803

例）短辺が100の場合の長辺

長辺 ＝ 100 × ${\dfrac {1+{\sqrt {5}}}{2}}$ ≒ 161.803

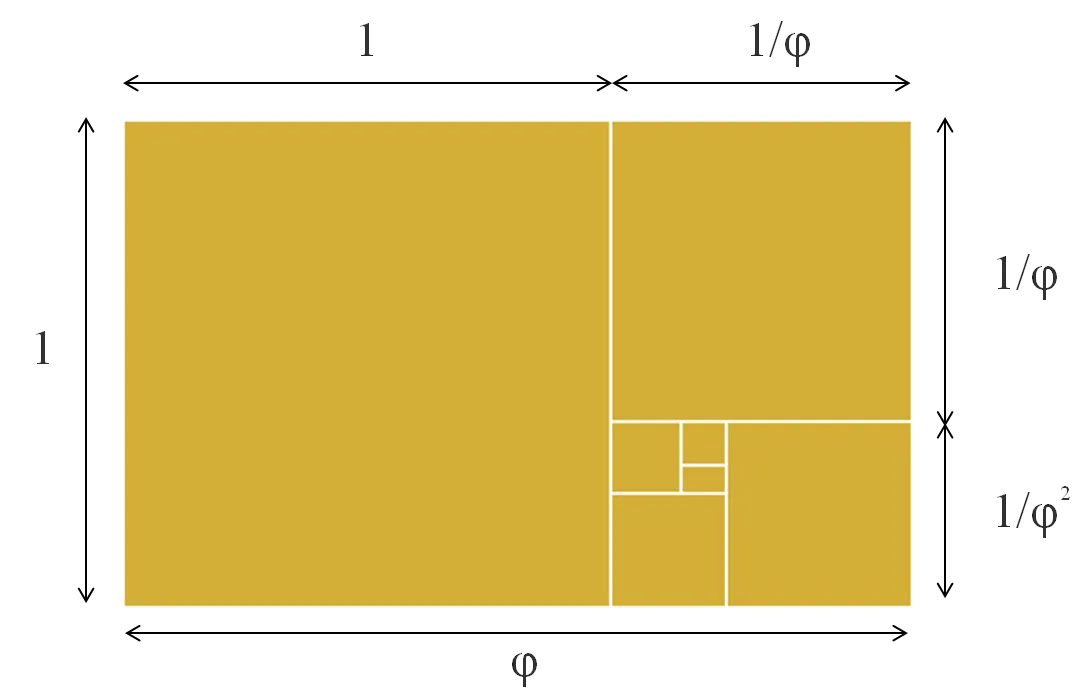
下図は黄金長方形と呼ばれるもので、辺の比が黄金比の長方形です。この黄金長方形から最大の正方形を除くと、残った長方形がまた黄金長方形になるので永遠に相似な図形ができていきます。

白銀比

白銀比（はくぎんひ）には以下の2つがあります。

① 貴金属比(第2貴金属比)

近似値は1:2.414。英語でsilver ratioなどと言った場合はこちらを指します。

② 大和比

${\displaystyle 1:{\sqrt {2}}{}\equiv {}{\sqrt {2}}:2}$ という性質から、紙の寸法などに用いられています。

なぜか日本人は黄金比より白銀比（大和比）を好むとされていて、古くから建造物などで採用されています。
例）法隆寺の金堂と五重塔、鳥獣戯画、東京スカイツリー、ドラえもん、etc

白銀比の計算例

例）長辺が100の場合の短辺

短辺 ＝ 100 ÷ ${\sqrt {2}}$ ≒ 70.711

例）短辺が100の場合の長辺

長辺 ＝ 100 × ${\sqrt {2}}$ ≒ 141.421

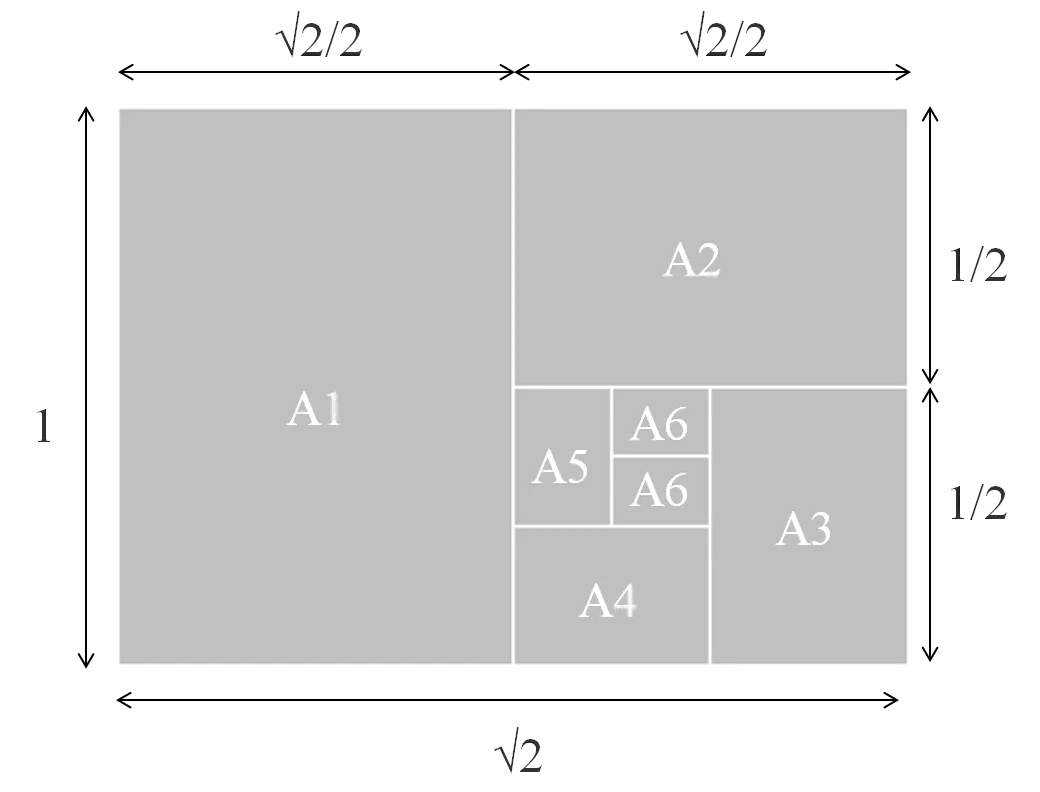
下図は辺の比が白銀比の長方形を二等分していったもので、すべての長方形が白銀比になっています。Ａ判Ｂ判などの紙の規格がこれです。